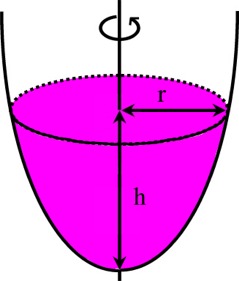
Tasokuvioita | ||
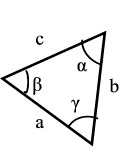
| Kolmio | ||
| Piirin puolikas | p = (a + b + c) / 2 | |
| Kulmien summa | α + β + γ = 180o | |
| Pinta-ala | 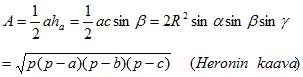 |
| Korkeusjana | ha = (bc / 2R) = (2A / a) = c sin β = b sin γ |
| Keskijana | |
| Kulmanpuolittaja | |
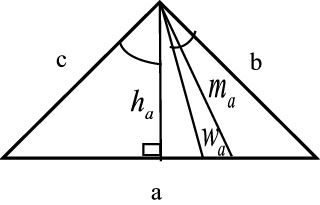
| Sisään piirretyn ympyrän säde |
| Ympäripiirretyn ympyrän säde |
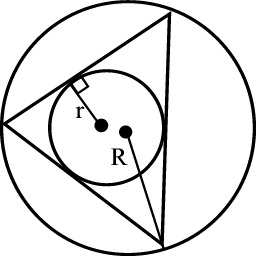
| Sinilause | |
| Kosinilause (laajennettu pythagoraan lause) b2 + c2 – a2 = 2bc cos α | |
| Tasasivuinen kolmio | ||
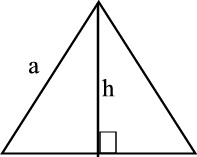
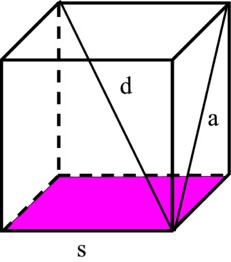
| Neliö | A = a2d = a√2 | 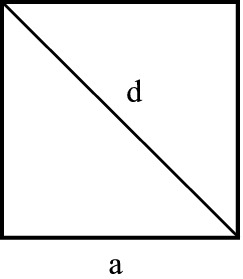 |
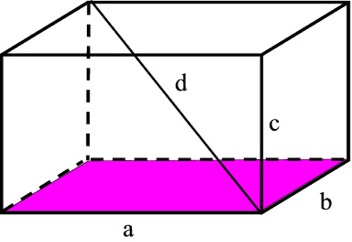
| Suorakulmio | A = ab d = √(a2 + b2) | 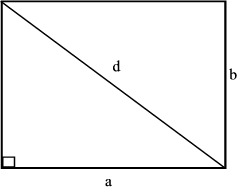 |
| Neljäkäs | A = ah = (1 / 2) d1d2 = a2 sin α | 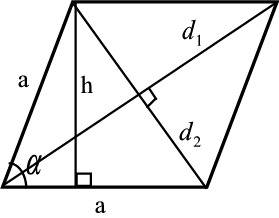 |
| Suunnikas | A = ah = ab sin β | 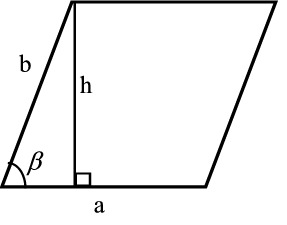 |
| Puolisuunnikas | A = (1 / 2) (a + b) h = mh | 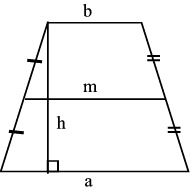 |
| Nelikulmio | A = (1 / 2) d1d2 sin φ | 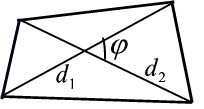 |
| Säännölliset monikulmiot Monikulmion sivu = a | ||||
| Sivujen luku- määrä | Sisään piirretyn ympyrän säde | Ympäri piirretyn ympyrän säde | Pinta-ala | Huomautuksia |
| 3 | (a √3) / 6 | (a √3) / 3 | (a2 √3) / 4 | tasasivuinen kolmio |
| 4 | a / 2 | (a √2) / 2 | a2 | neliö |
| 5 | lävistäjät jakavat toisensa jatkuvassa suhteessa | |||
| 6 | (a√3) / 2 | a | (3a2 √3) / 2 | koostuu kuudesta tasasivuisesta kolmiosta |
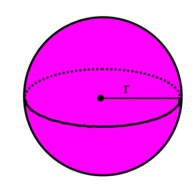
| Ympyrä | |
| kehän pituus = 2 π r pinta-ala A = π r2 | 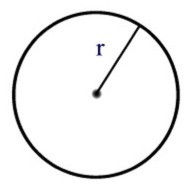 |
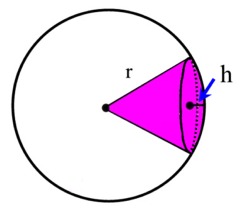
| sektorin kaaren pituus b = (α / 360o ) 2 π r sektorin pinta-ala A = (α / 360o ) π r2 = br / 2 | 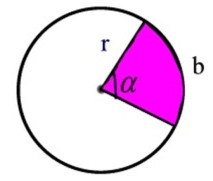 |
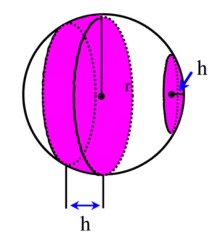
| segmentin pinta-ala | 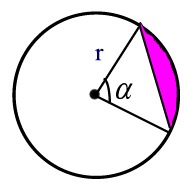 |
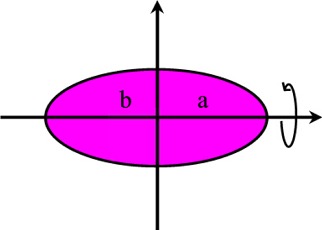
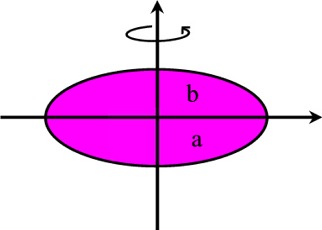
| Ellipsi | pinta-ala A = π ab | 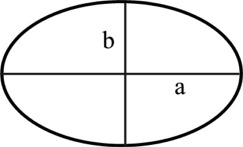 |
| Säännölliset monitahokkaat | |||||
| Tetraedri | Heksaedri = kuutio | Oktaedri | |||
| Monitahokkaan särmä = a | 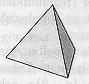 | 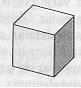 | 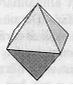 | ||
| rajapinta | 4 kolmiota | 6 neliötä | 8 kolmiota | ||
| pinta – ala | a2 √3 | 6 a2 | 2 a2 √3 | ||
| tilavuus | (a3 √2) / 12 | a3 | (a3 √2) / 3 | ||
| Dodekaedri | Ikosaedri | |
| Monitahokkaan särmä = a | 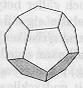 | 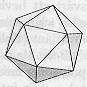 |
| rajapinta | 12 5-kulmiota | 20 kolmiota |
| pinta – ala | 3 a2 √ [ 5 (5 + 2 √5 ) ] | 5 a2 √3 |
| tilavuus | [ a3 (15 + 7 √5) ] / 4 | [ 5 a3 (3 + √5) ] / 12 |
| lähde |