Algebra


Prosentti ja prosenttiyksikkö

1 prosentti = 1 % = 1 / 100 = 0,01
1 promille =  1 ‰ = 1 / 1000 = 0,001
Prosenttiyksikkö on luku, jota käytetään ilmoittamaan suhteellisissa osuuksissa tapahtuneita muutoksia. Jos suureen osuus kokonaisuudesta on aluksi p % ja myöhemmin q %, on muutos q – p prosenttiyksikköä.
Esimerkki Jos lainan sijoituksen tuotto nousee 10 %:sta 12%:iin, on nousu prosenttiyksiköissä ilmaistuna 2 %-yksikköä ja prosenteissa ilmaistuna 20 %.

 

Reaalilukujen aksioomat

I Laskulait
1. Vaihdantalaki
2. Liitäntälaki
3. Osittelulaki
4. Nolla
5. Vastaluku
6. Ykkönen
7. Käänteisluku		a + b = b + a,   ab = ba
a + (b + c) = (a + b) + c,   a(bc) = (ab)c
a(b + c) = ab + ac
0 +a = a   (a on mielivaltainen)
x + a = 0   (merkintä x = -a)
1a = a      (a on mielivaltainen)
xa = 1       (merkintä x = 1/a, a ≠ 0
 II Järjestysaksioomat
Kaikille reaaliluvuille a, b ja c on voimassa
1. joko a < b tai a = b tai a > b
2. jos a < b ja b < c, niin a < c
3. ehdot a < b ja a + c < b + c ovat yhtäpitäviä
4. jos a > 0 ja b > 0, niin ab > o
III Täydellisyys aksiooma
Jokaisella rajoitettulla joukolla on pienin yläraja ja suurin alaraja.

 

Itseisarvo

Määritelmä
Graafinen tulkinta|a| = luvun a vastinpisteen etäisyys nollasta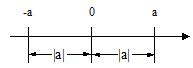
|a – b| = lukujen a ja b vastinpisteiden etäisyys nollasta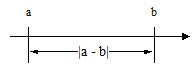

 

Rationaalilukujen laskutoimitukset

1. a / b = ka / kb, k ≠ 0laventaminen (→) ja supistaminen (←)
2. a / b + c / d = (ad + bc) / bdyhteenlasku (lavennus samannimisiksi)
3. a / b – c / d = (ad – bc) / bdvähennyslasku (lavennus samannimisiksi)
4. (a / b)(c / d) = ac / bdkertolasku
5. (a / b) / (c / d) = ad / bcjakolasku

 

Potenssi

EksponenttiMääritelmähuomautuksia
n = 1, 2, …an = a * a * …. *an tekijää, a = kantaluku
n = eksponentti
n = 0a0 = 1a ≠ 0, 00 ei määritelty
n = – p    (n ∈ _)a– p = 1 / apa ≠ 0, (a / b )– p = (b / a)p
 n = p / q   (n ∈ )a(p / q) =  a > 0

 

Potenssien laskusääntöjä

1. aman = am + nsamankantaisten potenssien tulo
2. am / an = am – n   (a ≠ 0)samankantaisten potenssien osamäärä
3. (ab)n = an * bntulon potenssi
4. (a / b)n = an / bn   (b ≠ 0)osamäärän potenssi
5. (am)n = amn = (an)mpotenssin potenssi
6. (a + b)2 = a2 + 2ab + b2binomin neliö
7. (a – b)2 = a2 – 2ab + b2binomin neliö
8. (a + b + c)2 = a2 + b2 +c2 + 2ab + 2ac +2bc          trinomin neliö
9.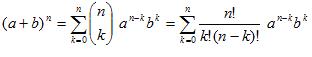Newtonin binomi kaava

 

Neliöjuuri

Määritelmä
on sellainen ei-negatiivinen luku, jonka neliö on a.
= b ⇔ b2 = a ja b ≥ 0
Reaaliuusehto
Vain ei-negatiivisilla reaaliluvuilla on neliöjuuri.
∈ ⇔ a ≥ 0

 

Kaavat
1. 4.
2. 5.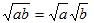
3. 6.

 

Laskutoimitukset
ToimitusKaavaSelitys
yhteenlaskub\sqrt{a}+c\sqrt{a} = (b+c)\sqrt{a}yhdistetään ne juuret, joissa on sama juurrettava
kertolaskuviedään saman juurimerkin alle
jakolaskuviedään saman juurimerkin alle
 lavennetaan juuri pois nimittäjästä

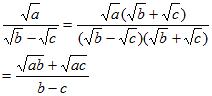Yleinen juuri

Kaavoissa juurrettavat a ≥ 0, sekä m, n ja k ovat positiivisia kokonaislukuja.
1. 5.
2. 6.
3. 7.
4.

 

Keskiarvo

Kahdelle luvulleYleisesti

 

Keskiverto

Jos, niinon a:n ja b:n keskiverto.
Yleisesti     

 

Polynomin jako tekijöihin

1. ab + ac = a(b + c)yhteinen tekijä
2. ac + ad +bc + bd = a(c + d) + b(c + d)
= (a + b) (c + d)		ryhmittely
3. a2 + 2ab + b2 = (a + b)2binomin neliö
    a2 – 2ab + b2 = (a – b)2
4. a2 – b2 = (a -b) (a +b)neliöiden erotus
    a3 – b3 = (a -b) (a2 + ab + b2)samankorkuisten
potenssien erotus
    a4 – b4 = (a2)2 – (b2)2 = (a – b) (a + b) (a2 + b2)
    a5 – b5 = (a – b) (a4 + a3b + a2b2 + ab3+ b4)
    a6 – b6 = (a3)2 – (b3)2 = (a3 – b3) (a3 + b3)
                 = (a – b) (a + b) (a2 + ab + b2) (a2 – ab + b2)
    …
    an – bn = (a – b) (an-1 + an-2b + … + abn-2 + bn-1)
5. a2 + b2    jaotonsamankorkuisten
potenssien summa
    a3 + b3 = (a + b) (a2 – ab + b2)
    a4 + b4 = (a2 + √2 ab + b2) (a2 – √a ab + b2)
    a5 + b5 = (a + b) (a4 – a3b + a2b2 – ab3 + b4)
    a6 + b6 = (a2)3 + (b2)3 = (a2 + b2) (a4 – a2b2 + b4)
    …
    an + bn = (a + b) (an-1 – an-2b + … +abn-2 + bn-1), n on pariton
Jos n on parillinen, niin an + bn ei jakaudu ensimmäisen asteen tekijöihin.
6. ax2 + bx + c = a (x – x1) (x – x2)tekijöihin jako
nollakohtin avulla
    anxn + an-1xn-1 + … + a1x + a0 = an (x – x1) (x – x2) … (x – xn)

 

Toisen asteen yhtälö

Normaalimuoto
ax2 + bx + c = 0   (a ≠ 0)
Yhtälön diskriminanttiD = b2 – 4ac
Jos D > 0, niin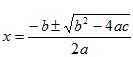
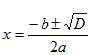(kaksi erisuurta reaalijuurta)
Jos D = 0(kaksoisjuuri)
Jos D < 0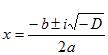(imaginaariset liittoluvut)
Suppea normaalimuoto
x2 + px + q = 0⇔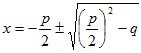
Juurien summa ja tulo
tai

 

Korkeamman asteen yhtälö

Normaalimuoto
anxn + an-1xn-1 + … + a1x + a0 = 0   (an ≠ 0 ja n ≥ 3)
Vasen puoli jakautuu tekijöihin
an (x – x1) (x – x2) … (x – xn) = 0
Yhtälöllä on n juurta x1, x2, … xn, joista osa voi olla keskenään yhtäsuuria, osa imaginaarisia liittolukuja.
Jos kokonaislukukertoimisella yhtälöllä on rationaalisia juuria, ne ovat muotoa , jossa p on jokin a0:n tekijä ja q on jokin an:n tekijä (luku itse, luku 1 sekä näiden vastaluvut mukaanlukien).

Determinantti

Kaksirivinen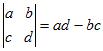 
Kolmirivinen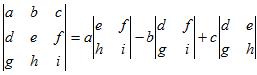 

 

Yhtälöpari

Normaalimuoto
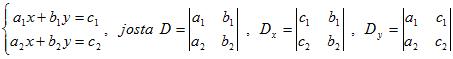Yhtälöparilla on yksikäsitteinen ratkaisu 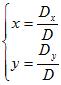, jos kerroindeterminantti D ≠ 0

 

Logaritmi

Määritelmäloga x = y ⇔ ay = xa = kantaluku (a >0, a ≠ 1)
x = numerus (x > 0)
Laskukaavatlog xy = log x + log y(kantaluku mielivaltainen)
log (x / y) = log x – log y
log xr = r log x
Kantaluvun vaihtologa x = (logb x / logb a)
Eräitä logaritmeja
loga 1 = 0loga a = 1loga ax = xaloga x = x

 

Raja-arvoja

Kaavoissa vakio a > 0
1.
2.
3.
4.
 5.
6.
7.
8.
9.

 

Lukujonoja ja summia

1. 1, 2, 3, …kokonaislukujono
     1 + 2 + 3 + … + n = (n(n +1)) / 2
2. 12 , 22, 32 …neliöjono
     12 + 22 + 32 + … + n2 = (n(n +1)(2n + 1)) / 6
3. 13, 23, 33, …kuutiojono
     13 + 23 + 33 + … + n3 = (n2(n +1)2) / 4
4. a1, a1 + d, a1 + 2d, …aritmeettinen jono
     an = a1 + (n – 1)dyleinen termi
    aritmeettinen summa
 5. a1, a1q, a1q2, …geometrinen jono
     an = a1qn-1yleinen termi
    S_n = \sum_{i=1}^{n} a_i= \frac{a_1(1-q^{n})}{1-q}, jos q ≠ 1geometrinen summa
     Sn = na1, jos q = 1
 6. suppeneva geometrinen sarja

 

Sarjakehitelmä

1.
     jossa α ∈ , ja n ∈  ja , suppenee kun
|x| < 1
2.
     Saadaan edellisestä, kun α = n ∈ , ks. Newtonin binomikaava (linkki)
3. ex = 1 + (x / 1!) + (x2 / 2!) + (x3 / 3!) + …
4. ln (1 + x) = x – (1 /2)x2 + (1 / 3)x3 – (1 / 4)x4 + …– 1 < x ≤ 1
5. sin x = x – (x3 / 3!) + (x5 / 5!) – (x7 / 7!) + …
6. cos x = 1 – (x2 / 2!) + (x4 / 4!) – (x6 / 6!) + …
7. tan x = x + (x3 / 3) + (2x5 / 15) + (17x7 / 315) + …|x| < (π / 2)
8. cot x = (1 / x) – (x / 3) – (x3 / 45) – (2x5 / 945) – …0 < |x| < π
9. arcsin x = x + (x3 / 6) + (3x5 / 40) + (15x7 / 280) + …|x|<1
10. arctan x = x – (x3 / 3) + (x5 / 5) – (x7 / 7) + …|x|<1

 

Talousmatematiikkaa

Koron korko
Kn = Kqn , jossa
Kn= kasvanut pääoma
K = pääoma
q = korkotekijä = 1 + (p / 100)
p = korkoprosentti korkokaudelta
n = korkokausien lukumäärä
Jos vuodessa on m korkokautta, niin kaavoissa
p = vuotuinen korkoprosentti / m.
Jatkuva korko
Kt = Ke(p / 100) t, jossap = vuotuinen korkoprosentti
t = aika vuosina
Annuiteetti- eli tasaerälaina
A = Kqn ( (1 – q) / (1 – qn) ), jossaA = annuiteetti eli tasaerä
K = lainapääoma
Vk = Kqk – A ( (1 – qk) / (1 – q) ), jossaVk = jäljellä oleva lainamäärä K:nnen lyhennyksen jälkeen

 

Kompleksiluvut

= { z | z = a + bi,    a, b ∈, i2 = -1 }
Imaginaariyksikköä i vastaa kompleksitason piste (0, 1).
ReaaliosaRe z = a
ImaginaariosaIm z = b
Kompleksilukuaz = a + bi vastaa kompleksitason piste (a, b)
Identtiisyysz1 = z2 ⇔ Re z1 = Re z2 ja Im z1 = Im z2
Nimityksiäb ≠ 0 ⇒ z imaginaarinen
a = 0 ja b ≠ 0 ⇒ z = bi puhtaasti imaginaarinen
b = 0 ⇒ z = a reaaliluku
Vastaluku –z = -a – bi
Liittoluku  = a – bi
 
Itseisarvo eli moduli 
Käänteisluku
Laskutoimituksetz1 z2 = (a1 a2) + (b1 b2) i
kz = ka + kbi
z1z2 = (a1a2 – b1b2) + (a1b2 + a2b1) i
    (i:n poisto nimittäjästä)

 

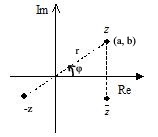
Napakoordinaattiesitys
z = r (cosφ + i sin φ) = reiφ
Itseisarvo |z| = r.
Vaihekulma eli argumentti φ = arg z valitaan tavallisesti väliltä – π < φ ≤ π
(jaksona 2π). Kun z = a + bi ja a ≠ 0, on tan φ = (b / a).
 Laskutoimitukset
 z1z2 = r1r2 [ cos (φ1 + φ2) + i sin (φ1 + φ2) ]
 zn = rn [cos nφ + i sin nφ]
 (z1 / z2) = (r1 / r2) [ cos (φ1 – φ2) + i sin (φ1 – φ2) ]
 
 Moivren kaava (cos φ + i sin φ)n = cos nφ + i sin nφ
 Eulerin kaava = cos φ + i sin φ  Erikoisesti: = -1

 

Boolen algebraa

Aksioomat
1. Vaihdantalakia + b = b + a, ab = ba
2. Liitäntälakia + (b + c) = (a + b) + c,   a(bc) = (ab)c
3. Osittelulaita(b + c) = ab + ac,   a + bc = (a + b)(a + c)
4. Yhteenlaskun neutraalialkioa + 0 = a
5. Kertolaskun neutraalialkioa * 1 = a
6. Alkion ja komplementin summaa + = 1
7. Alkion ja komplementin tuloa * = 0
Laskutoimitukset
1. Summa ja tulo alkion itsensä kanssaa + a = a,   a * a = a
2. Tulo 0:n kanssaa * 0 = 0
3. Summa 1:n kanssaa + 1 = 1
4. Komplementin komplementti = a