Normaalijakauma


 

Normaalijakauman kertymäfunktio

\Phi (x)=\frac{1}{\sqrt{2\pi }}\int_{-\infty}^{x}{e}^{-\frac{{t}^{2}}{2}}dt

Φ(a) = P(X ≤ a), Φ(-a) = 1 – Φ(a)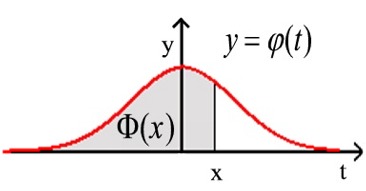

lähde

 

x.00.01.02.03.04.05.06.07.08.09
.0.5000.5040.5080.5120.5160.5190.5239.5279.5319.5359
.1.5398.5438.5478.5517.5557.5596.5636.5675.5714.5753
.2.5793.5832.5871.5910.5948.5987.6026.6064.6103.6141
.3.6179.6217.6255.6293.6331.6368.6406.6443.6480.6517
.4.6554.6591.6628.6664.6700.6736.6772.6808.68446879
.5.6915.6950.6985.7019.7054.7088.7123.7157.7190.7224
.6.7257.7291.7324.7357.7389.7422.7454.7486.7517.7549
.7.7580.7611.7642.7673.7704.7734.7764.7794.7823.7852
.8.7881.7910.7939.7969.7995.8023.8051.8078.8106.8133
.9.8159.8186.8212.8238.8264.8289.8315.8340.8365.8389
1.0.8413.8438.8461.8485.8508.8513.8554.8577.8529.8621
1.1.8643.8665.8686.8708.8729.8749.8770.8790.8810.8830
1.2.8849.8869.8888.8907.8925.8944.8962.8980.8997.9015
1.3.9032.9049.9066.9082.9099.9115.9131.9147.9162.9177
1.4.9192.9207.9222.9236.9215.9265.9279.9292.9306.9319
1.5.9332.9345.9357.9370.9382.9394.9406.9418.9429.9441
1.6.9452.9463.9474.9484.9495.9505.9515.9525.9535.9545
1.7.9554.9564.9573.9582.9591.9599.9608.9616.9625.9633
1.8.9641.9649.9656.9664.9671.9678.9686.9693.9699.9706
1.9.9713.9719.9726.9732.9738.9744.9750.9756.9761.9767
2.0.9772.9778.9783.9788.9793.9798.9803.9808.9812.9817
2.1.9821.9826.9830.9834.9838.9842.9846.9850.9854.9857
2.2.9861.9864.9868.9871.9875.9878.9881.9884.9887.9890
2.3.9893.9896.9898.9901.9904.9906.9909.9911.9913.9916
2.4.9918.9920.9922.9925.9927.9929.9931.9932.9934.9936
2.5.9938.9940.9941.9943.9945.9946.9948.9949.9951.9952
2.6.9953.9955.9956.9957.9959.9960.9961.9962.9963.9964
2.7.9965.9966.9967.9968.9969.9970.9971.9972.9973.9974
2.8.9974.9975.9976.9977.9977.9978.9979.9979.9980.9981
2.9.9981.9982.9982.9983.9984.9984.9985.9985.9986.9986
3.0.9987.9987.9987.9988.9988.9989.9989.9989.9990.9990
3.1.9990.9991.9991.9991.9992.9992.9992.9992.9993.9993
3.2.9993.9993.9994.9994.9994.9994.9994.9995.9995.9995
3.3.9995.9995.9995.9996.9996.9996.9996.9996.9996.9997
3.4.9997.9997.9997.9997.9997.9997.9997.9997.9997.9998
lähde

 

Φ(x)0.900.950.9750.9900.9950.9990.99950.99990.99995
x1.28161.64491.96002.32642.57583.09023.29053.71903.8906

 

Taulukon käyttö esimerkkejä
1. P(X ≤ 1,35) = Φ(1,35) ≈ 0,9115
2. P(-0,55 ≤ X ≤ 1,50) = Φ(1,50) – Φ (-0,55) = Φ(1,50) – 1 + Φ(0,55)
≈ 0,9332 – 1 + 0,7088 = 0,6420
3. Jos X ~ N(12,6), niin Z = ( (X – 12) / 6 ) ~ N(0,1). Tällöin P(X ≥ 15)
= 1 – P(X < 15) = 1 – P( Z ( ( 15 – 12) / 6) ) = 1 – Φ(0,5) ≈ 1 – 0,6915
= 0,3085
Normitusperiaate

 

Normaalijakauman tiheysfunktio

 \phi (x)={\frac{1}{\sqrt{2\pi }}}^{{e}^{-\frac{1}{2}}{x}^{2}}
 lähde
x0123456789
0,10,399397391381368352333312290266
0,2242218194171150130111094079066
0,3054044035028022018014010008006
0,4004003002002001001001000000000

 

Χ2– taulukko

 {X}^{2}=\sum_{i=1}^{k}\frac{{\left({o}_{i}-{e}_{i} \right)}^{2}}{{e}_{i}},jossaoi = i:nnen luokan havaittujen arvojen frekvenssi
ei = i:nnen luokan teoreettinen frekvenssi
k = luokkien lukumäärä
Yhden muuttujan tapauksessa vapausasteluku n = s – 1 ja kahden muuttujan tapauksessa n = (s – 1)(r – 1). Kaavoissa r on rivien lukumäärä ja s sarakkeiden lukumäärä.

 

Vapausaste-
luku		p = 0,10
(10%)		p = 0,05
(5%)		p = 0,025
(2,5%)		p = 0,01
(1%)		p = 0,001
(0,1%)
12.7063.8415.0246.63510.828
24.6055.9917.3789.21013.816
36.2517.8159.34811.34516.266
47.7799.48811.14313.27718.467
59.23611.07012.83315.08620.515
610.64512.59214.44916.81222.458
712.01714.06716.01318.47524.322
813.36215.50717.53520.09026.125
914.68416.91919.02321.66627.877
1015.98718.30720.48323.20929.588
1117.27519.67521.92024.72531.264
1218.54921.02623.33726.21732.910
1319.81222.36224.73627.68834.528
1421.06423.68526.11929.14136.123
1522.30724.99627.48830.57837.697
1623.54226.29628.84532.00039.252
1724.76927.58730.19133.40940.790
1825.98928.86931.52634.80542.312
1927.20430.14432.85236.19143.820
2028.41231.41034.17037.56645.315
2129.61532.67135.47938.93246.797
2230.81333.92436.78140.28948.268
2332.00735.17238.07641.63849.728
2433.19636.41539.36442.98051.179
2534.38237.65240.64644.31452.620
2635.56338.88541.92345.64254.052
2736.74140.11343.19546.96355.476
2837.91641.33744.46148.27856.892
2939.08742.55745.72249.58858.301
3040.25643.77346.97950.89259.703
lähde
Taulukon käyttöesimerkki
Kun vapausasteluku n = 4 ja tarkasteltava riskitaso p = 0,05 :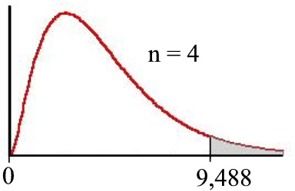
lähde
Jos testimuuttujan arvo Χ2 > 9,488, niin voidaan (5%:n riskitasolla) päätellä, että havaintojen jakauma ei noudata teoreettista jakaumaa.

 

t-taulukko

vapausaste-
luku		p = 0,20
(20%)		p = 0, 10
(10%)		p = 0,05
(5%)		p = 0,025
(2,5%)		p = 0,01
(1%)		p = 0,001
(0,1%)
13.0786.31412.70625.45263.656636.578
21.8862.9204.3036.2059.92531.600
31.6382.3533.1824.1775.84112.924
41.5332.1322.7763.4954.6048.610
51.4762.0152.5713.1634.0326.869
61.4401.9432.4472.9693.7075.959
71.4151.8952.3652.8413.4995.408
81.3971.8602.3062.7523.3555.041
91.3831.8332.2622.6853.2504.781
101.3721.8122.2282.6343.1694.587
111.3631.7962.2012.5933.1064.437
121.3561.7822.1792.5603.0554.318
131.3501.7712.1602.5333.0124.221
141.3451.7612.1452.5102.9774.140
151.3411.7532.1312.4902.9474.073
161.3371.7462.1202.4732.9214.015
171.3331.7402.1102.4582.8983.965
181.3301.7342.1012.4452.8783.922
191.3281.7292.0932.4332.8613.883
201.3251.7252.0862.4232.8453.850
211.3231.7212.0802.4142.8313.819
221.3211.7172.0742.4052.8193.792
231.3191.7142.0692.3982.8073.768
241.3181.7112.0642.3912.7973.745
251.3161.7082.0602.3852.7873.725
261.3151.7062.0562.3792.7793.707
271.3141.7032.0522.3732.7713.689
281.3131.7012.0482.3682.7633.674
291.3111.6992.0452.3642.7563.660
301.3101.6972.0422.3602.7503.646
401.3031.6842.0212.3292.7043.551
501.2991.6762.0092.3112.6783.496
601.2961.6712.0002.2992.6603.460
701.2941.6671.9942.2912.6483.435
801.2921.6641.9902.2842.6393.416
901.2911.6621.9872.2802.6323.402
1001.2901.6601.9842.2762.6263.390
1201.2891.6581.9802.2702.6173.373
1501.2871.6551.9762.2642.6093.357
2001.2861.6531.9722.2582.6013.340
∞1.2821.6451.9602.2422.5763.291
lähde

 

Binomikertoimet (Pascalin kolmio)

 \begin{pmatrix} n\\k \end{pmatrix}=\frac{n(n-1)...(n-k+1)}{k!}=\frac{n!}{k!(n-k)!}0! = 1! = 1
n
01
111
2121
31331
414641
515101051
61615201561
7172135352171
818285670562881
9193684126126843691
101104512021025221012045101

 

Newtonin binomikaava

 {\left(a+b \right)}^{n}=\sum_{k=0}^{n}\begin{pmatrix} n\\k \end{pmatrix}{a}^{n-k}{b}^{k}
Esimerkki {\left(a+b \right)}^{4} =\begin{pmatrix} 4\\0 \end{pmatrix}{a}^{4}+\begin{pmatrix} 4\\1 \end{pmatrix}{a}^{3}b+\begin{pmatrix} 4\\2 \end{pmatrix}{a}^{2}{b}^{2}=\begin{pmatrix} 4\\3 \end{pmatrix}a{b}^{3}+\begin{pmatrix} 4\\4 \end{pmatrix}{b}^{4}
 = 1 a4 + 4 a3 b + 6 a2b2 + 4 ab3 + 1 b4
 = a4 + 4 a3 b + 6 a2b2 + 4 ab3 + b4