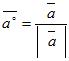Vektorilaskenta


Laskutoimitukset

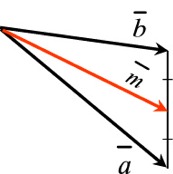
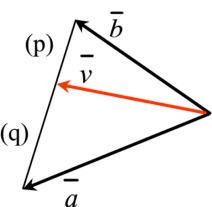
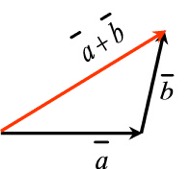
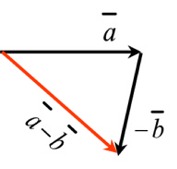
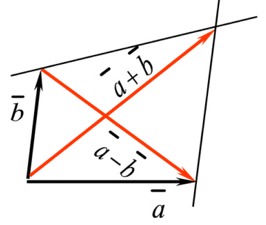
Summa ja erotus
Luku • vektori
\tiny \left|k\bar{a} \right|=\left|k \right|\left|\bar{a} \right|     ja

\tiny k\bar{a} ↑ ↑  \tiny \bar{a} , jos k > 0
\tiny k\bar{a} ↑ ↓  \tiny \bar{a} , jos k < 0
\tiny k\bar{a} = \tiny \bar{0} , jos k = 0

 

Määritelmiä

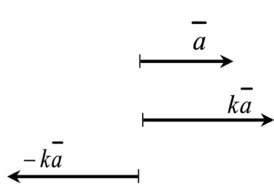
nollavektori\tiny \bar{0} on vektori, jonka suunta on epämääräinen ja pituus 0.
yksikkövektorion \tiny \bar{a}: n suuntainen ja sen pituus on 1,
vastavektori – \tiny \bar{a} on \tiny \bar{a}: n pituinen ja sille vastakkaissuuntainen, joten
\tiny \bar{a} + (- \tiny \bar{a}) = \tiny \bar{0}
paikkavektori \tiny \vec{OA}=\bar{r} on origon O ja pisteen A yhdysvektori
mediaanivektori\tiny \bar{m}=\frac{\bar{a}+\bar{b}}{2}
jakosuhdevektori \tiny \bar{v}=\frac{p\bar{a}+q\bar{b}}{p+q}

 

Komponenttiesitys

\tiny \bar{a} = ax \tiny \bar{i} + ay \tiny \bar{j} + az \tiny \bar{k} ,    \tiny \bar{b} = bx \tiny \bar{i} + by \tiny \bar{j} + bz \tiny \bar{k} ,     \tiny \bar{c} = cx \tiny \bar{i} + cy \tiny \bar{j} + cz \tiny \bar{k}
\tiny \bar{i}, \tiny \bar{j} ja \tiny \bar{k} ovat xyz -koordinaatiston yksikkövektorit.
1. paikkavektori = \tiny \bar{a}, jos A = ( ax , ay , az )
2. pituus \tiny \left|\bar{a} \right|=\sqrt{{{a}_{x}}^{2}+{{a}_{y}}^{2}+{{a}_{z}}^{2}}=\sqrt{\bar{a}\cdot \bar{a}}
3. identtisyys \tiny \bar{a} = \tiny \bar{b} ⇔ ( \tiny \bar{a} ↑ ↑ \tiny \bar{b} ∧ |\tiny \bar{a}| = \tiny \left|\bar{b} \right| ) ⇔ (ax = bx ∧ ay = by ∧ az + bz)
4. summa \tiny \bar{a} \tiny \pm \tiny \bar{b} = (ax \tiny \pm bx) \tiny \bar{i} + (ay \tiny \pm by) \tiny \bar{j} + (az \tiny \pm bz) \tiny \bar{k}
5. luku • vektori k\tiny \bar{a} = kax \tiny \bar{i} + kay \tiny \bar{j} + kaz \tiny \bar{k}
6. pistetulo
(skalaaritulo)		\tiny \bar{a} • \tiny \bar{b} = |\tiny \bar{a}| \tiny \left|\bar{b} \right| cos (\tiny \bar{a} , \tiny \bar{b}) = ax bx + ay by + az bz
7. kohtisuoruus\tiny \bar{a} ⊥ \tiny \bar{b} ⇔ \tiny \bar{a} • \tiny \bar{b} = 0 , kun \tiny \bar{a} , \tiny \bar{b} ≠ \tiny \bar{0}
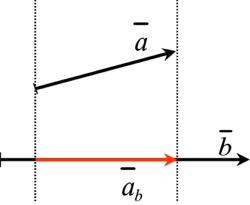
8. välinen kulma\tiny cos\:\left(a,\: b \right)=\frac{\bar{a}\cdot \bar{b}}{\left|\bar{a} \right|\left|\bar{b} \right|},     0o ≤   (\tiny \bar{a}, \tiny \bar{b}) ≤180o
9. skalaariprojektio \tiny {a}_{b}=\frac{\bar{a}\cdot \bar{b}}{\left|\bar{b} \right|}
10. vektoriprojektio \tiny {\bar{a}}_{b}=\frac{\bar{a}\cdot \bar{b}}{\bar{b}\cdot \bar{b}}\: \bar{b}
 
11. ristitulo
(vektoritulo)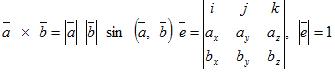
 
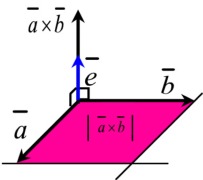12. yhdensuuntaisuus
13. suunnikkaan ala
14. skalaarikolmiotulo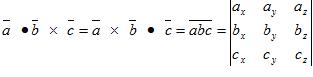
15. särmiön tilavuus\tiny V=\left|\bar{abc} \right|,tetraedrin tilavuus\tiny =\frac{1}{6}V
 
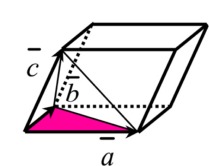16. vektorit samassa tasossa  \tiny \Leftrightarrow \left|\bar{abc} \right|=0,\: kun\: \bar{a},\: \bar{b},\: \bar{c}\neq \bar{0}
17. vektorikolmitulo \tiny \bar{a}\times \left(\bar{b}\times \bar{c} \right)=\left(\bar{a}\cdot \bar{c} \right)\bar{b}-\left(\bar{a}\cdot \bar{b} \right)\bar{c}
 \tiny \left(\bar{a}\times \bar{b} \right)\times \bar{c}=\left(\bar{a}\cdot \bar{c} \right)\bar{b}-\left(\bar{b}\cdot \bar{c} \right)\bar{a}