Trigonometria


Absoluuttinen kulmayksikkö

 Määritelmä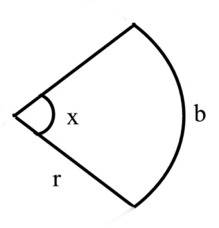x=\frac{b}{r} Yhteysπ rad = 180o

 

Muistikolmiot

 

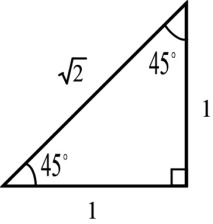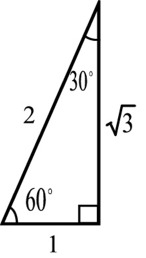Trigonometriset funktiot

Määritelmät
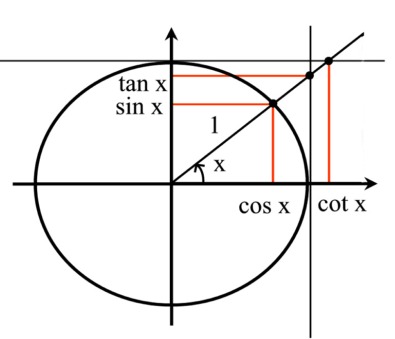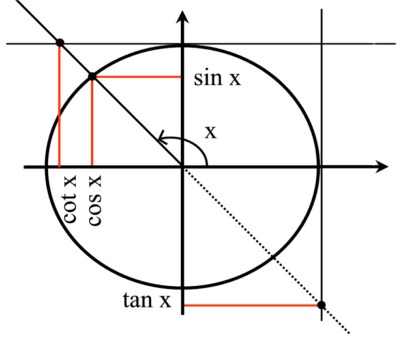Ominaisuuksia
FunktioMääritysjoukkoArvojoukkoPerusjaksoSymmetria
sin[-1, 1]2 πpariton
cos[-1, 1]2 πparillinen
tanx ≠ ( π / 2 ) + n ππpariton
cotx ≠ n ππpariton
Kuvaajat
y = sin x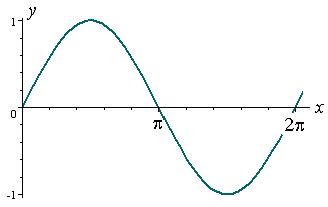
y = cos x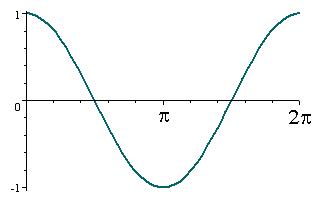
y = tan x
y = cot x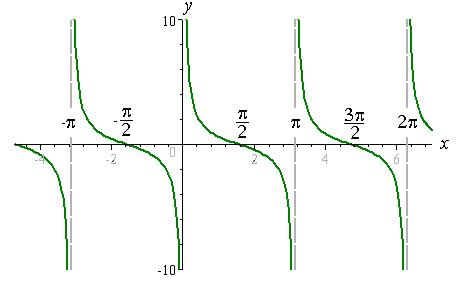
lähde

 

Arkusfunktiot

Määritelmät
 \int(x)=sin\: x, -\frac{\pi }{2}\leq x\leq \frac{\pi }{2}⇔ \int_{}^{-1}(x)=arcsin\: x
 \int (x)=cos\: x, 0\leq x\leq \pi \int_{}^{-1}(x)=arccos\: x
 \int (x)=tan\: x, -\frac{\pi }{2}\leq x\leq \frac{\pi }{2} \int_{}^{-1}(x)=arctan\: x
Kuvaajat
y = arcsin x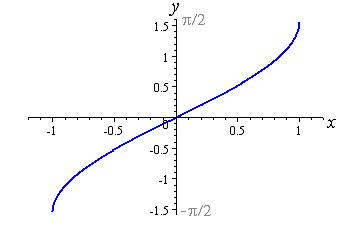
y = arccos x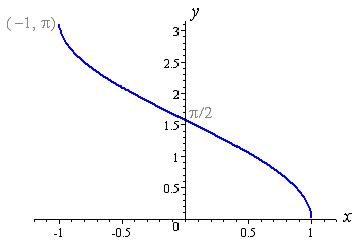
y = arctan x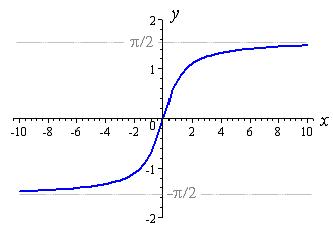
y = arccot x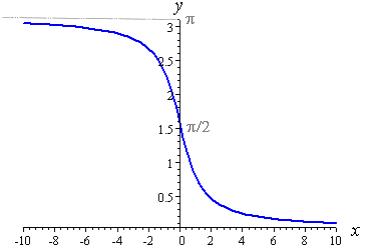

 

Ominaisuuksia
FunktioMääritysjoukkoArvojoukko
arcsin[-1, 1] \tiny \left[-\frac{\pi }{2},\frac{\pi }{2}\right]
arccos[-1, 1][ 0, π ]
arctan \tiny ]\right -\frac{\pi }{2},\frac{\pi }{2} \left[

 

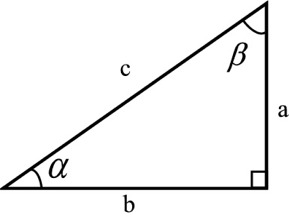
Suorakulmaisen kolmion trigonometria

1. a2 + b2 = c2   (Pythagoraan lause)2. A = (1 / 2) ab3. β = 90o – α
4. sin α = (a / c)5. cos α = (b / c)6. tan α = (a / b)7. cot α = (b / a)

Peruskaavat

1. sin2 x + cos2 x = 12. tan x = sin x / cos x3. cot x = 1 / tan x

 

Merkkikaaviot

sin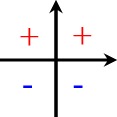cos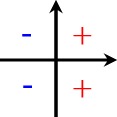
tan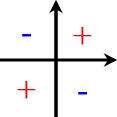cot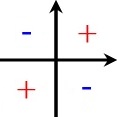

 

Trigonometristen funktioiden väliset yhteydet

Etumerkkivaihtoehdoista valitaan merkkikaavion mukainen kyseiseen neljännekseen kuuluva etumerkki.
 \tiny 1.\: sin\: x =\pm \sqrt{1-{cos}^{2}x}=\pm \frac{tan\: x}{\sqrt{1+{tan}^{2}x}}=\pm \frac{1}{\sqrt{1+{cot}^{2}x}}
 \tiny 2.\: cos\: x =\pm \sqrt{1-{sin}^{2}x}=\pm \frac{1}{\sqrt{1+{tan}^{2}x}}=\pm \frac{cot\: x}{\sqrt{1+{cot}^{2}x}}
 \tiny 3.\: tan\: x =\frac{1}{cot\: x}=\pm \frac{sin\: x}{\sqrt{1-{sin}^{2}x}}=\pm \frac{\sqrt{1-{cos}^{2}x}}{cos\: x}
 \tiny 4.\: cot\: x =\frac{1}{tan\: x}=\pm \frac{\sqrt{1-{sin}^{2}x}}{sin\: x}=\pm \frac{cos\: x}{\sqrt{1-{cos}^{2}x}}

 

Palautuskaavat

1. sin x = -sin (-x) = cos ( (π / 2) – x) = sin (π – x) = sin (x + n 2 π)
2. cos x = cos (-x) = sin ( (π / 2) – x) = -cos (π – x) = cos (x + n 2 π)
3. tan x = -tan (-x) = cot ( (π / 2) – x) = -tan (π – x) = tan (x + n π)
4. cot x = -cot (-x) = tan ( (π / 2) – x) = -cot (π – x) = cot (x + n π)

 

Kaksinkertaiset kulmat

1. sin 2x = 2 sin x cos x
2. cos 2x = cos2 x – sin2 x = 2 cos2 x – 1 = 1 – 2 sin2 x
3. tan 2x = 2 tan x / (1 – tan2 x)  = 2 / (cot x – tan x)
4. cot 2x = (cot2 x -1) / 2 cot x  = (cot x – tan x) / 2

 

Kolminkertaiset kulmat

1. sin 3x = 3 sin x – 4 sin3 x = sin x (4 cos2 x – 1)
2. cos 3x = 4 cos3 x – 3 cos x = cos x (1 – 4 sin2 x)
3. tan 3x = (3 tan x – tan3 x) / ( 1 – 3 tan2 x)
4. cot 3x = (cot3 x – 3 cot x) / (3 cot2 x – 1)

 

Puolikkaat kulmat

Etumerkkivaihtoehdoista valitaan merkkikaavion mukainen kyseiseen neljännekseen kuuluva etumerkki.
 \tiny 1.\: sin\: \frac{x}{2}=\pm \sqrt{\frac{1-cos\: x}{2}}
 \tiny 2.\: cos\: \frac{x}{2}=\pm \sqrt{\frac{1+cos\: x}{2}}
 \tiny 3.\: tan\: \frac{x}{2}=\pm \sqrt{\frac{1-cos\: x}{1+cos\: x}}=\frac{sin\: x}{1+cos\: x}=\frac{1-cos\: x}{sin\:x}
 \tiny 4.\: cot\: \frac{x}{2}=\pm \sqrt{\frac{1+cos\: x}{1-cos\: x}}=\frac{sin\: x}{1-cos\: x}=\frac{1+cos\: x}{sin\:x}

 

Trigonometristen funktioiden potensseja

1. sin2 x = (1 / 2) (1 – cos 2x)4. cos3 x = (1 / 4) (cos 3x + 3 cos x)
2. cos2 x = (1 / 2) (1 + cos 2x)5. sin4 x = (1 / 8) (cos 4x – 4 cos 2x + 3)
3. sin3 x = (1 / 4) (3 sin x – sin 3x)6. cos4 x = (1 / 8) (cos 4x + 4 cos 2x + 3)

 

Summakaavoja

Kaksoismerkeistä ylemmät vastaavat toisiaan, samoin alemmat.
 \tiny 1.\: sin\: (x\pm y)=sin\: x\: cos\: y\pm cos\: x\:sin\: y
 \tiny 2.\: cos\: (x\pm y)=cos\: x\: cos\: y\mp sin\: x\:sin\: y
 \tiny 3.\: tan\: (x\pm y)=\frac{tan\: x\pm tan\: y}{1\mp tan\: x\: tan\: y}
 \tiny 4.\: cot\: (x\pm y)=\frac{cot\: x\: cot\: y\mp1 }{cot\: y\pm cot\: x}
 \tiny 5.\: sin\: x+sin\: y=2\: sin\frac{x+y}{2}\: cos\frac{x-y}{2}
 \tiny 6.\: sin\: x-sin\: y=2\: cos\frac{x+y}{2}\: sin\frac{x-y}{2}
 \tiny 7.\: cos\: x+cos\: y=2\: cos\frac{x+y}{2}\: cos\frac{x-y}{2}
 \tiny 8.\: cos\: x-cos\: y=-2\: sin\frac{x+y}{2}\: sin\frac{x-y}{2}
 \tiny 9.\: tan\: x\pm tan\: y=\frac{sin\: x\pm y}{cos\:x \: cos\: y}
 \tiny 10.\: cot\: x\pm cot\: y=\frac{sin\: y\pm x}{sin\:x \: sin\: y}
 \tiny 11.\: cos\: x\pm sin\: x=\sqrt{2}\: sin\left(\frac{\pi }{4}\pm x \right)=\sqrt{2}\: cos\left(\frac{\pi }{4}\mp x \right)

 

Peruskaavoja

1. sin x = sin y⇔x = y + n 2 π ∨ x = π – y + n 2 π, n ∈
2. cos x = cos y⇔x = \tiny \pm y + n 2 π, n ∈
3. tan x = tan y⇔x = y + n π, n ∈
4. cot x = cot y⇔ x = y + n π, n ∈